Week 1 — Introduction to Cryptography
Contents:
Section 1: Basic Concepts ---- Video 01: Background ---- Video 02: Introduction to Cryptography ---- Video 03: Good Crypto Bad Crypto ---- Video 04: Number Theory ---- Video 05: Large Numbers are Really Large ---- Video 06: Kerckhoffs’s Principle ---- Video 07: Random Numbers, Hash Functions, and Encryption Section 2: Encryption Basics ---- Video 08: Encryption History ---- Video 09: Building Blocks for Encryption Algorithms ---- Video 10: Modes of Encryption ---- Video 11: Encryption Properties, Cryptanalysis, Stenography
Section 1: Basic Concepts
Video 01: Background
Cryptography (as a term):
- crypto == secret
- graphy == writing
The history of cryptography:
Number Theory
- 1’500 BCE.
- 300 BCE (Euclid), prime numbers etc.
Cryptography
- Ancient history ➜ 50 BCE, Ceasar cipher / subtitution cipher
- History ➜ 1550 CE, more ciphers (VIGNERE cipher).
- WW2 ➜ most advancement towards the modernization of cryptography.
Note: Navajo code talkers (not really crypto, more like steganography)
Modern cryptography:
- Started around 1970.
- Number theory became more applied.
Notable/famous algorithms and their replacements:
- DES (digital encryption standard) ➜ AES (advanced encryption standard).
- RSA (Ron Rivest, Adi Shamir, and Leonard Adleman) (public-key crypto system) ➜ RSA, ECC.
- MD5 (message digest algorithm version 5) ➜ SHA (secure hash algorithm).
Notes:
- Theoritical cryptography ➜ mathematicians.
- Applied cryptography ➜ computer science (course focus).
Forms of data:
- At rest.
- In motion (course focus).
Primary concepts / techniques used throughout cryptography:
- Random numbers.
- Hash functions.
- Encryption …
- Symmetric.
- Asymmetric.
Note: Underlying concept is large numbers.
Video 02: Introduction to Cryptography
Three basic principles:
- Random numbers.
- Hash functions.
- Encryptions.
Used for:
- Authentication.
- Password management.
- Digital signatures.
- Digital certificates.
Crypto protocols are considered:
- Brittle (rigid and likely to break).
- Subtle.
- Error prone.
What is a hash function?
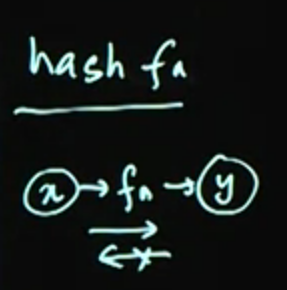
Example provided: coint toss over the phone.
Video 03: Good Crypto Bad Crypto
Does cryptography work?
- Yes – there are established respected algorithms.
- No – most algorithms that have been developed in the past have been broken.
Maxim to good crypto: Do not invent, reuse.
Cryptography ==/== Security
- Crypto is unbreakable.
- However, there are other attack vectors.
- For example, what if your key management is broken?
DES (Digital Encryption Standard):
- First open source crypto algorithm.
- NSA / NIST (developed by IBM).
- Never broken, but it has outlived its usefulness (56 bits).
DES ➜ AES (advanced encryption standard)
- AES block sizes: 128 / 256 / 512.
MD5 (Message Digest Version 5)
- Invented by Rivest.
- Replaced by SHA (Secure Hash Algorithm).
Video 04: Number Theory
Numbers (in crypto) are Integers, Positive, Finite.
Prime numbers are important (e.g., 2, 3, 5, 7, etc.).
Two large primes:
- p * q = N
- Cannot be factorized / reversed.
- Used in public key encryption (e.g., RSA).
Prime numbers are infinite proof:

What is true about prime numbers as we move toward infinity?
As we move toward infinity, the distance between two primes increases.
Algorithms that are more CS: AES, SHA.
Algorithms that ahs more number theory: RSA, ECC, DH.
What is the definition of a block?
Data broken into fixed-sized chunks with a constant number of bits per block.
Note: Input block, output block and key length might not be of the same size.
Video 05: Large Numbers are Really Large
n-bit numbers:
- Length = 2n.
- Range = [ 0, (2n)-1 ].


Video 06: Kerckhoffs’s Principle
- The system must be practically, if not mathematically, indecipherable;
- It should not require secrecy, and it should not be a problem if it falls into enemy hands;
- It must be possible to communicate and remember the key without using written notes, and correspondents must be able to change or modify it at will;
- It must be applicable to telegraph communications;
- It must be portable, and should not require several persons to handle or operate;
- Lastly, given the circumstances in which it is to be used, the system must be easy to use and should not be stressful to use or require its users to know and comply with a long list of rules.
What is the takeaway?
- No secret algorithms.
- Keys can be secret.
Side effect?
- Many eyes theory.
Prove it?
- Only for asymmetric key encryption.
- Symmetric key encryption is considered ad-hoc.
- Generally though, it is not feasible.
Remark: Designers don’t see flaws.
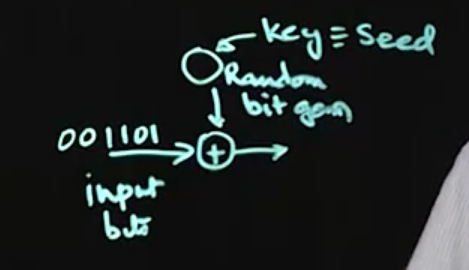
Video 07: Random Numbers, Hash Functions, and Encryption
Random Numbers:
- They satisfy statistical tests.
- They require a seed that is random.
Hash Functions (one way function):
- Produces fixed sized output from variable size input.
- Deterministric.
- Not reversible.
- For crypto, it needs to be collision resistant.
Encryption (one way trapdoor function):
- Lossless (has to be, unlike hash).
- n-bit input ➜ n-bit output.
Note: Symmetric encryption is considered Ad-hoc, while asymmetric encryption is more number theory.
Section 2: Encryption Basics
Video 08: Encryption History
Ceasar Cipher (50 BCE)
- 2 shift forward to encrypt.
- 2 shift backward to decrypt.
- mono alphabetic cipher.
To decrypt, use:
- Brute force.
- Letter frequency analysis.
Vegenre cipher (1553)
- Poly-alphabetic cipher.

Kasiski 1863, broke the cipher: Look for certain pairs of characters in cipher text.
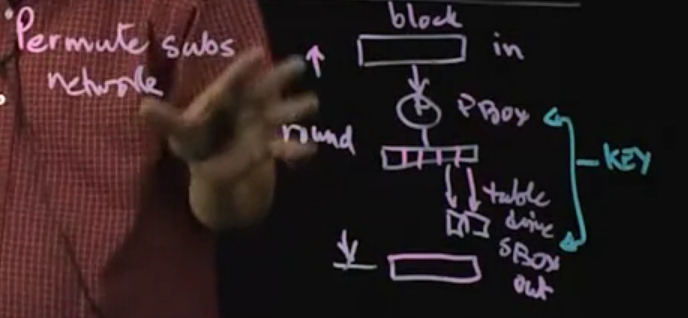
Video 09: Building Blocks for Encryption Algorithms
Symmetric encryption

How to do it?
- Jumble / permute.
- Subtitute.
Shannon principles:
Confusion ➜ one bit of output is derived from many bits of input.
Diffusion ➜ changing one bit of input causes a change in ~ 50% of the output.
Feistel cipher:
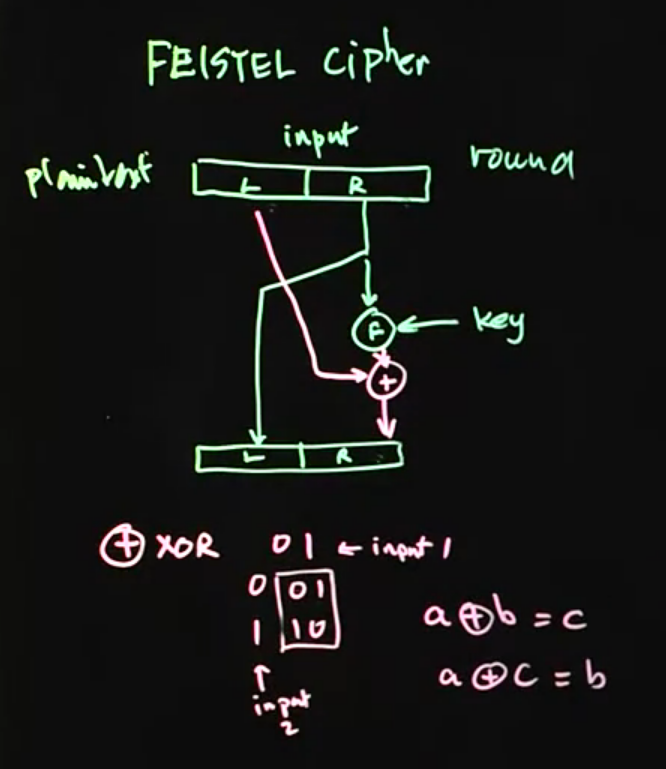
What is F?
- Non linear Feistel function.
- Uses pbox and sbox.
Note: It is used in DES.
Video 10: Modes of Encryption
Symmetric encryption:
- DES: 56
- AES: 128, 256, 512
- They are considered mono-alphabetic.
Modes of encryption:
- EBC == electronic code book ➜ mono alphabetic
- CBC == cipher block chaining

Stream encryption:
- Does it one bit at a time.
- Example, RC4 cipher.
Key strength == How much work you have to do to break the cipher.
- for an n-bit key.
- you need (roughly) 2n iteration to brute force it.
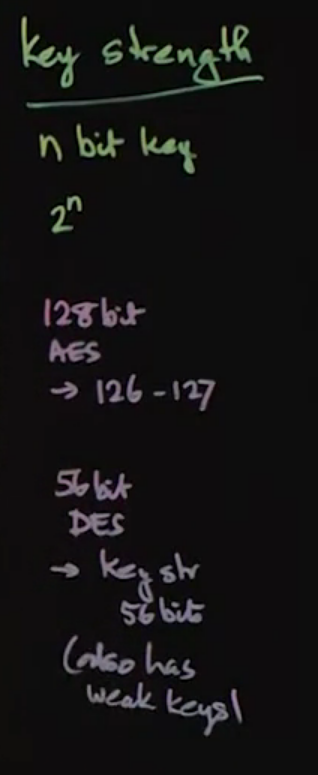
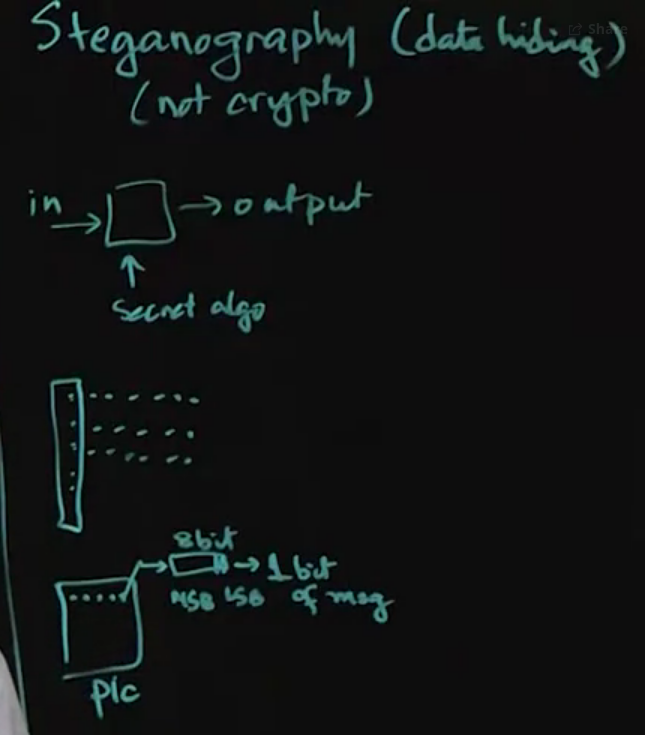
Video 11: Encryption Properties, Cryptanalysis, Stenography

Cryptanalysis: Find weaknesses in cipher.
Typs of attacks:
- Given the ciphertext, find key / plaintext.
- Given the ciphertext + plaintext, find key.
- Come up with plaintext, observe the ciphertext, find key.
- Linear cryptanalysis (LC + linear approximation of SBoxes).
- Differential cryptanalysis.
Steganography =/= Crypto, it is data hiding.