Week 6 — RSA and Number Theory
Contents:
Week 6 Live Event Section 1: Proof of RSA ---- Video 01: RSA and the sets Zn and Z*n ---- Video 02: Closure of the Set Z*n ---- Video 03: Properties of Z*n ---- Video 04: How to Show RSA Works Section 2: Primality Testing, Fast Exponentiation, and Computing Private Keys ---- Video 05: Fast Exponentiation ---- Video 06: Probabilistic Algorithms and Fermat’s Primality Test ---- Video 07: Miller-Rabin Primality Testing ---- Video 08: Generating Private Keys
Week 6 Live Event









Section 1: Proof of RSA
Video 01: RSA and the sets Zn and Z*n

Video 02: Closure of the Set Z*n

Video 03: Properties of Z*n

Video 04: How to Show RSA Works
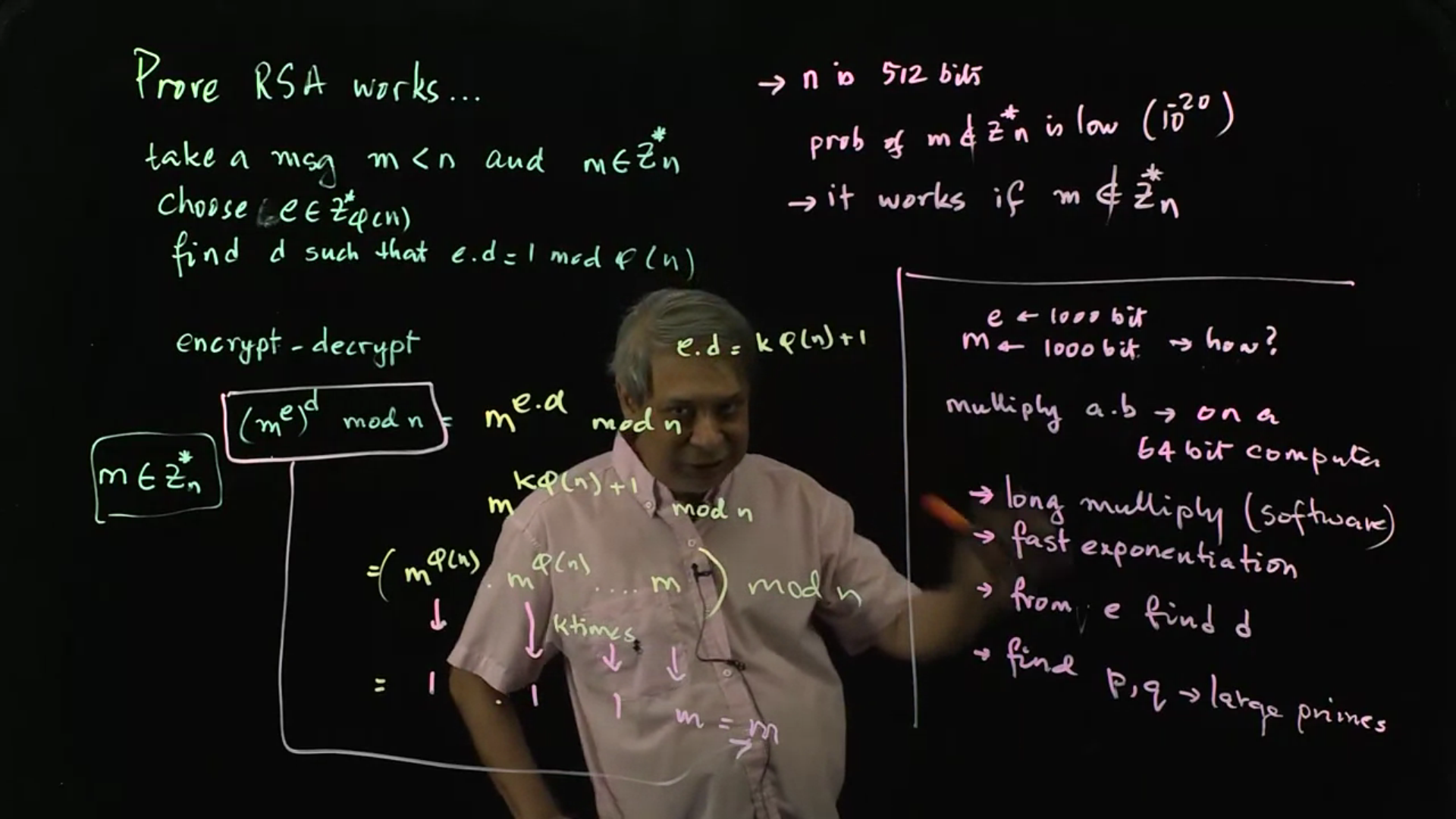
Section 2: Primality Testing, Fast Exponentiation, and Computing Private Keys
In order to actually implement RSA, it must be able to do fast exponentiation, find prime numbers and compute public and private keys. This section discusses the details involved in implementing RSA.
Lecture Video Guide
Fast Exponentiation: Since both encryption and decryption in RSA require exponentiating a large number by a large power, the exponentiation has to be fast. Note that the exponentiation time cannot be linear in the value of the exponent, but must be in the order of the logarithm of the exponent.
Probabilistic Algorithms and Fermat’s Primality Test: We can use probabilistic primality tests to find a prime number; this lecture demonstrates probabilistic algorithms and how to use Fermat’s primality test.
Miller-Rabin Primality Testing: Miller-Rabin is yet another primality test that can be slipped into the Fermat’s test algorithm to enhance the effectiveness of the test for primality.
Generating Private Keys: Now that we have two primes (p and q) and the modulus (p x q), how do we find the encryption and decryption keys, e and d?
Video 05: Fast Exponentiation

Video 06: Probabilistic Algorithms and Fermat’s Primality Test

Video 07: Miller-Rabin Primality Testing
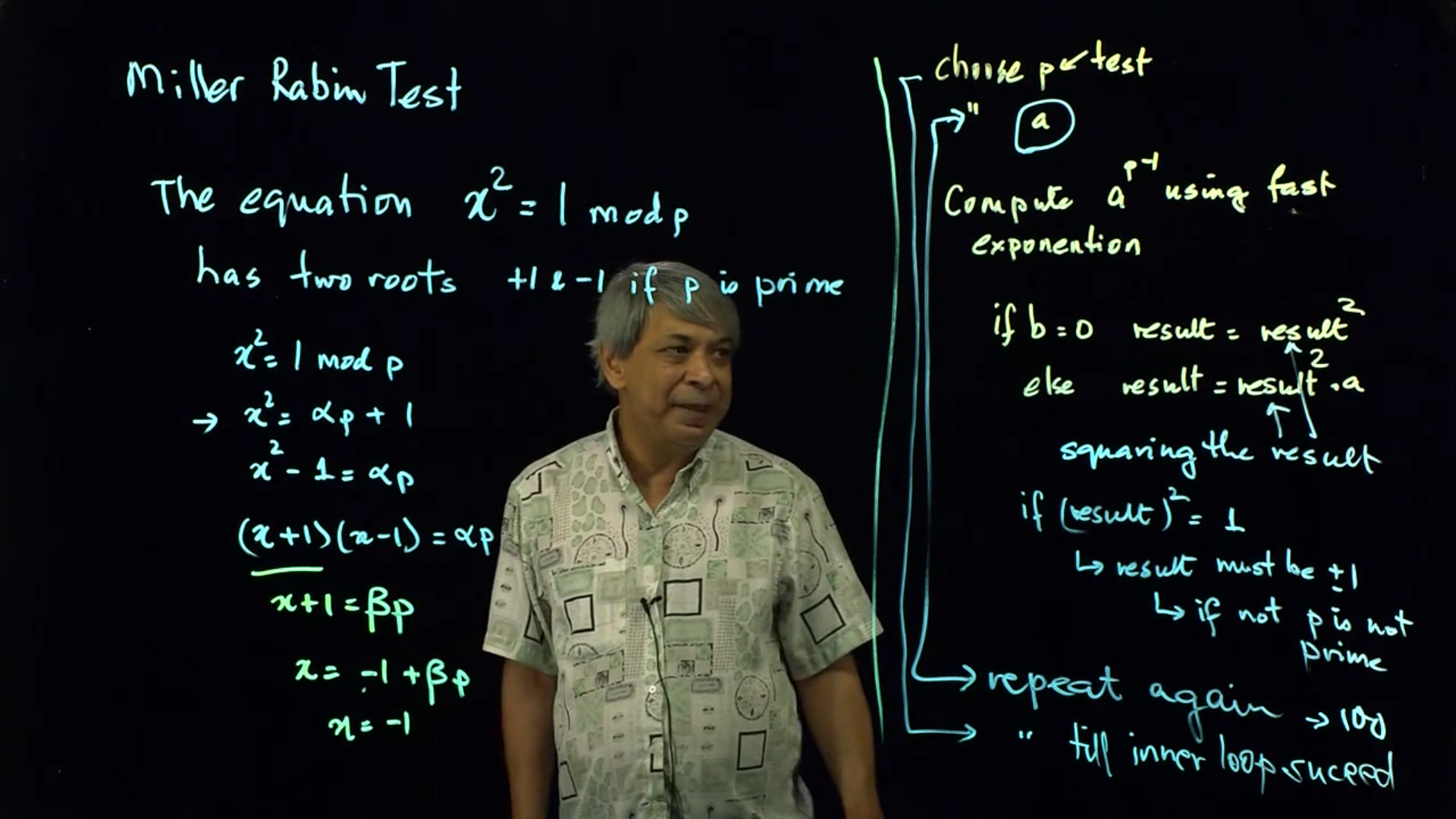
Video 08: Generating Private Keys
