Week 7 — Advanced Cryptographic Protocols
Contents:
Section 1: Cut and Choose ---- Video 01: Blind Signatures ---- Video 02: Anonymous Money Orders ---- Video 03: Graph Isomorphism and Zero Knowledge Proofs ---- Video 04: FFS Proof of Identity ---- Video 05: Oblivious Transfer Section 2: Cryptographic Techniques ---- Video 06: Secret Splitting and Secret Sharing ---- Video 07: Bit Commitment ---- Video 08: Timestamping ---- Video 09: Dining Cryptographers ---- Video 10: Commutative Encryption and Mental Poker
Section 1: Cut and Choose
What is the fair way to slice a cake in two parts to share between two people? Let one person cut the cake and the other person choose their piece to eat. This simple method can be used in cryptography to create Anonymous Money Orders (using another scheme called Blind Signatures).
Lecture Video Guide
Blind Signatures: If Alice sends an encrypted document to Bob and asks Bob to sign the unencrypted document without telling Bob the decryption key, Bob will not be able to sign. However, in this lecture, we discuss how the Blind Signature scheme makes this impossible task possible.
Anonymous Money Orders: The Blind Signature scheme sounds dangerous, but is indeed useful in many applications (such as the anonymous money orders). This lecture shows how a bank can remain safe, and Alice can still get money orders anonymously.
Graph Isomorphism and Zero Knowledge Proofs: Yet another application of the Cut and Choose method is its use in Zero Knowledge Proofs. This lecture uses graph isomorphism as an example to explain Zero Knowledge Proofs.
FFS Proof of Identity: The Zero Knowledge method can be used for authentication. This lecture discusses one such authentication algorithm: the FFS (Feige Fiat Shamir).
Oblivious Transfer: Suppose Alice has a few digital things and Bob takes one, without Alice knowing which one. Even Bob does not get a choice. This lecture discusses how this is possible through oblivious transfer.
Video 01: Blind Signatures
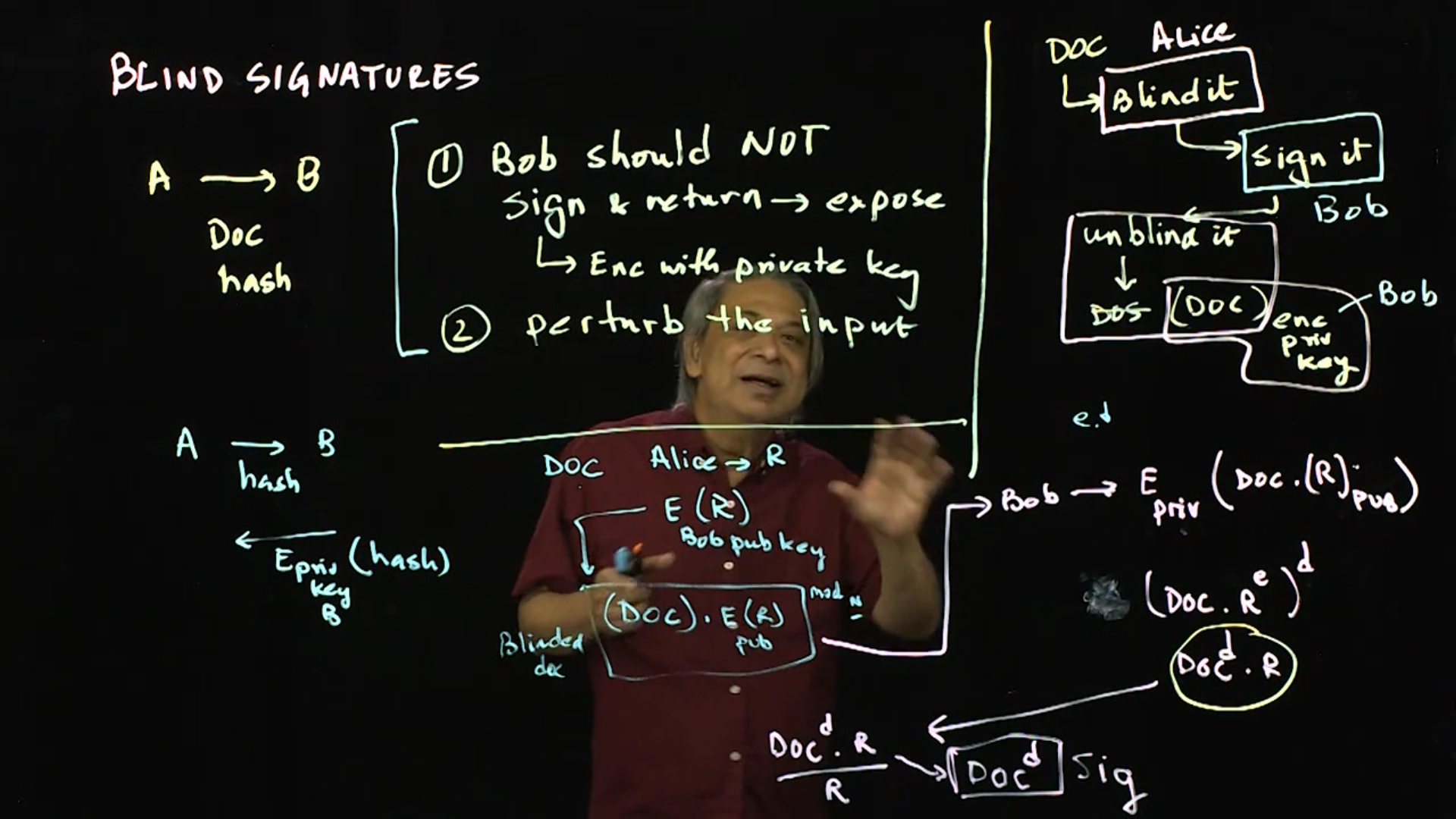
Video 02: Anonymous Money Orders

Video 03: Graph Isomorphism and Zero Knowledge Proofs

Video 04: FFS Proof of Identity
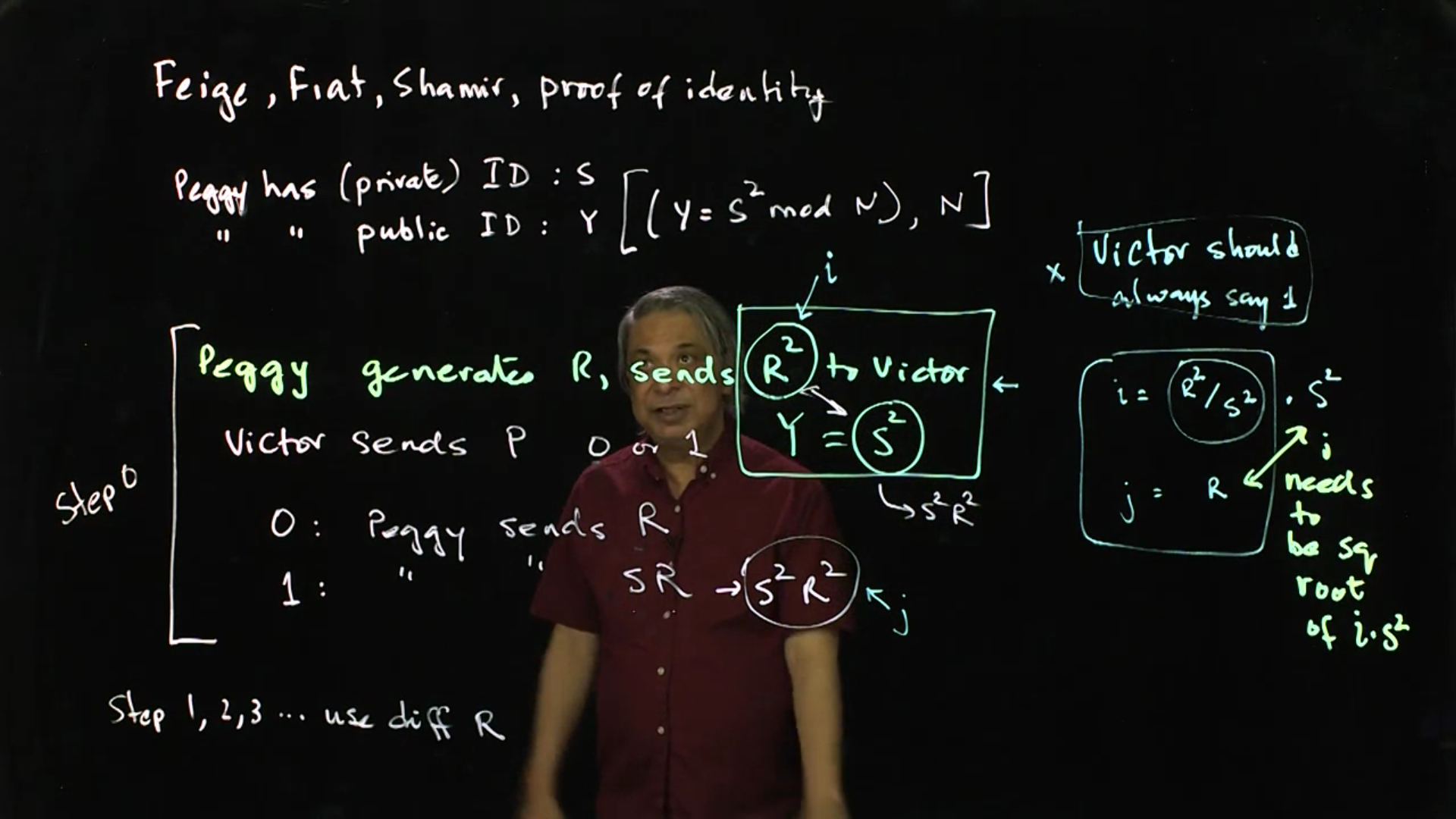
Video 05: Oblivious Transfer
==> not well understood
==> I really don’t understand it
In cryptography, an oblivious transfer (OT) protocol is a type of protocol in which a sender transfers one of potentially many pieces of information to a receiver, but remains oblivious as to what piece (if any) has been transferred.
The first form of oblivious transfer was introduced in 1981 by Michael O. Rabin.1 In this form, the sender sends a message to the receiver with probability 1/2, while the sender remains oblivious as to whether or not the receiver received the message. Rabin’s oblivious transfer scheme is based on the RSA cryptosystem. A more useful form of oblivious transfer called 1–2 oblivious transfer or “1 out of 2 oblivious transfer”, was developed later by Shimon Even, Oded Goldreich, and Abraham Lempel,2 in order to build protocols for secure multiparty computation.
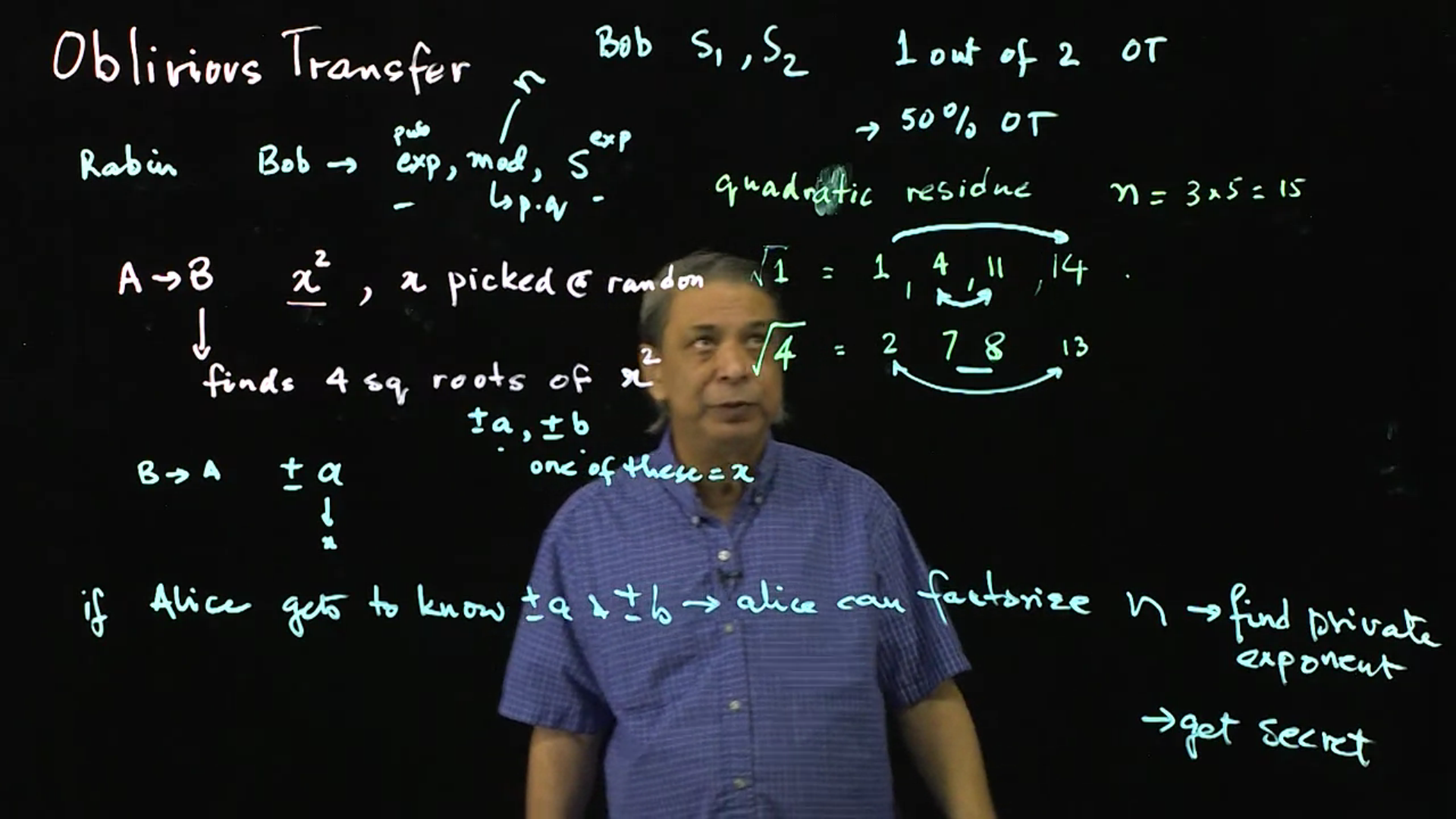

Section 2: Cryptographic Techniques
This section of the course builds on the topics covered in Cut and Choose with more advanced cryptography topics. The topics include simple secret splitting schemes, committing to decisions that cannot be undone later, secure timestamping and commutative encryption. This section will also introduce and discuss the entertaining Dining Cryptographers problem.
Lecture Video Guide
Secret Splitting and Secret Sharing: Given a secret, how can we segment it into multiple secrets (or blobs) such that each blob does not reveal any part of the secret, but some or all of the blobs do reveal the secret? This lecture presents two techniques that approach this problem.
Bit Commitment: Suppose Alice flips a coin and picks heads or tails. Alice will tell Bob of her choice later, but cannot change her mind later. How does Bob enforce that what Alice picks is what she will say later? Use bit commitment.
Timestamping: Timestamping is simple and useful, but timestamping is not secure, as it can be changed. If Alice writes a document in Year X, decades later can she show it was written in year X and not written later and back dated? It can be harder than it appears. This lecture covers two methods for achieving the goal.
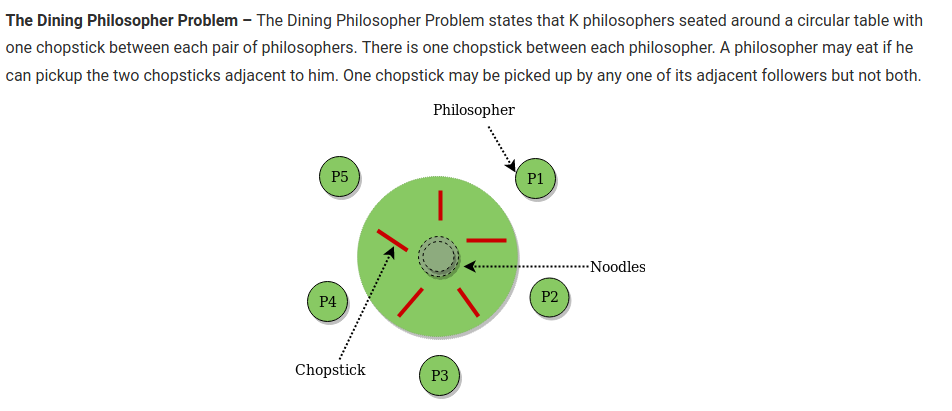
Dining Cryptographers: Five cryptographers are having dinner, at a round table. The NSA might be involved. What could go wrong?
Commutative Encryption and Mental Poker: This lecture defines the notion of commutative encryption and uses it in a game of dealing cards for poker.
Video 06: Secret Splitting and Secret Sharing
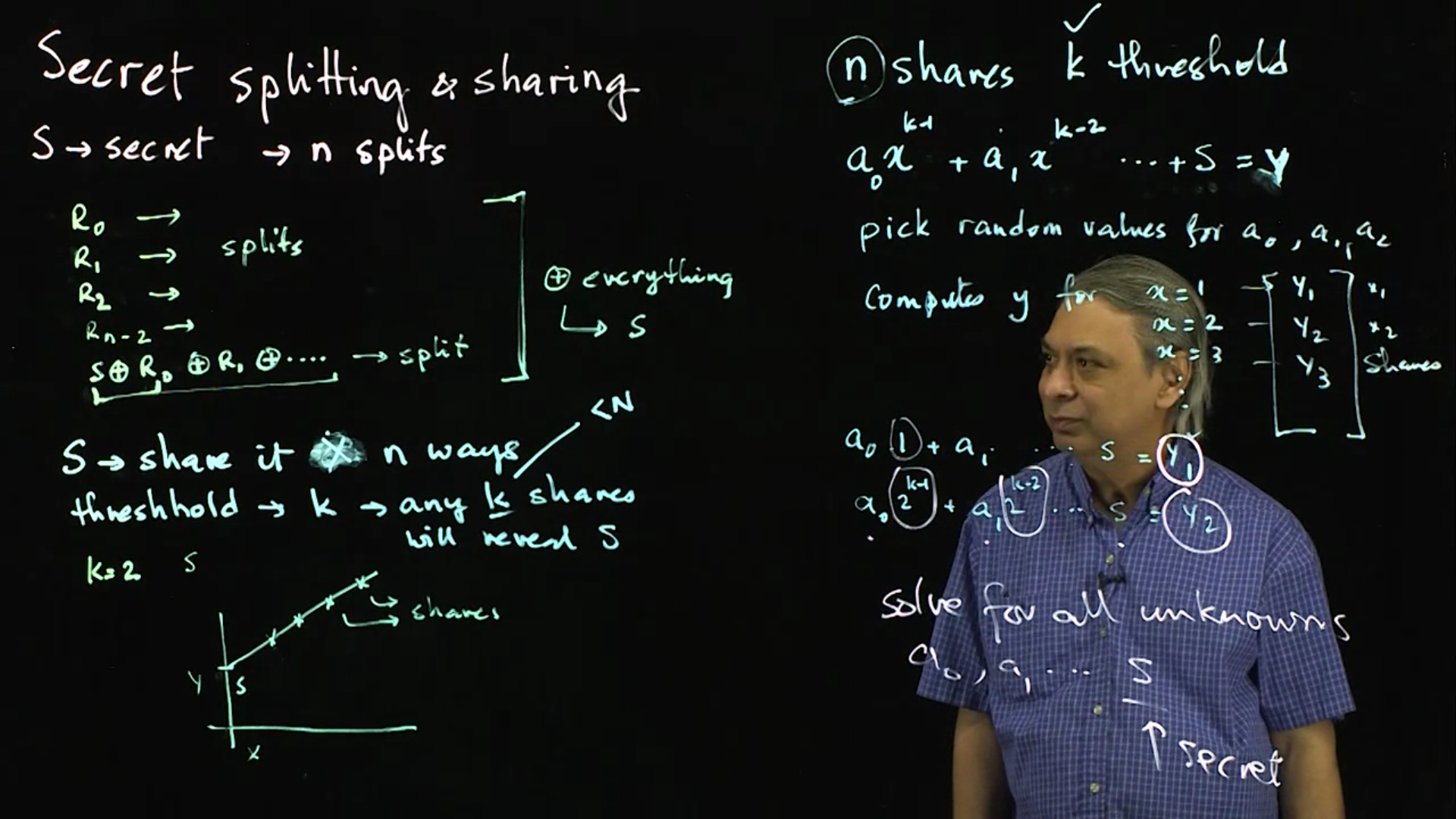
Video 07: Bit Commitment

Video 08: Timestamping

Video 09: Dining Cryptographers

Video 10: Commutative Encryption and Mental Poker


